Advertisements
Advertisements
प्रश्न
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
पर्याय
True
False
उत्तर
This statement is True.
Explanation:
Let EAF be tangent to the circumcircle of ∆ABC.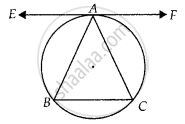
To prove: EAF ॥ BC
We have, ∠EAB = ∠ACB ...(i) [Angle between tangent and chord is equal to angle made by chord in the alternate segment]
Here, AB = AC
⇒ ∠ABC = ∠ACB ...(ii)
From equation (i) and (ii), we get
∠EAB = ∠ABC
∵ Alternate angles are equal.
⇒ EAF ॥ BC
APPEARS IN
संबंधित प्रश्न
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

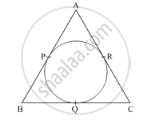
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
In the given circle with diameter AB, find the value of x.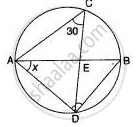
The ratio between the circumference and diameter of any circle is _______
The length of tangent from an external point on a circle is always greater than the radius of the circle.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

