Advertisements
Advertisements
प्रश्न
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

उत्तर
Given, ∠OAB = 30° and ∠OCB = 57°
In ΔAOB, AO = OB ...[Both are the radius of a circle]
⇒ ∠OBA = ∠BAO = 30° ...[Angles opposite to equal sides are equal]
In ΔAOB,
⇒ ∠AOB + ∠OBA + ∠BAO = 180° ...[By angle sum property of a triangle]
∴ ∠AOB + 30° + 30° = 180°
∴ ∠AOB = 180° – 2(30°)
= 180° – 60°
= 120° ...(i)
Now, in ΔAOB,
OC = OB ...[Both are the radius of a circle]
⇒ ∠OBC = ∠OCB = 57° ...[Angles opposite to equal sides are equal]
In ΔOCB,
∠COB + ∠OCB + ∠CBO = 180° ...[By angle sum property of triangle]
∴ ∠COB = 180° – (∠OCB + ∠OBC)
= 180° – (57° + 57°)
= 180° – 114°
= 66° ...(ii)
From equation (i), ∠AOB = 120°
⇒ ∠AOC + ∠COB = 120°
⇒ ∠AOC + 66° = 120° ...[From equation (ii)]
∴ ∠AOC = 120° – 66° = 54°
APPEARS IN
संबंधित प्रश्न
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
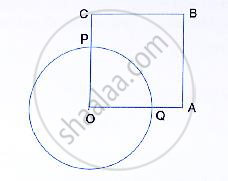
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

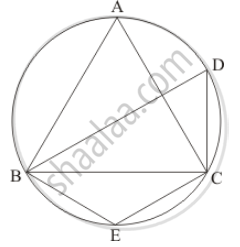
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
The diameter of a circle is 12.6 cm. State, the length of its radius.
The ratio between the circumference and diameter of any circle is _______
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______