Advertisements
Advertisements
प्रश्न
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
उत्तर
Given: ΔABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C.
To prove: PA is an angle bisector of ∠BPC.
Construction: Join PB and PC.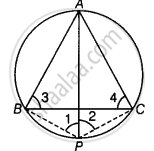
Proof: Since, ΔABC is an equilateral triangle.
∠3 = ∠4 = 60°
Now, ∠1 = ∠4 = 60° ...(i) [Angles in the same segment AB]
∠2 = ∠3 = 60° ...(ii) [Angles in the same segment AC]
∴ ∠1 = ∠2 = 60°
Hence, PA is the bisector of ∠BPC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
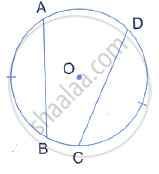
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
The point of concurrence of all angle bisectors of a triangle is called the ______.
Use the figure given below to fill in the blank:
R is the _______ of the circle.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

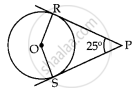
In the given figure, if ZRPS = 25°, the value of ZROS is ______
A line through the point of contact and passing through centre of the circle is known as ______
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB