Advertisements
Advertisements
Question
Can the length of a chord of a circle be greater than its diameter ? Explain.
Solution
No, the length of the chord cannot be greater than the diameter of the cirlce as the diameter of a circle is the greatest chord of that circle.
APPEARS IN
RELATED QUESTIONS
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
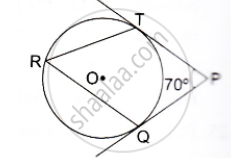
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
In the given figure, if ∠ABC = 45°, then ∠AOC =
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
The ratio between the circumference and diameter of any circle is _______
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.