Advertisements
Advertisements
Question
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Solution
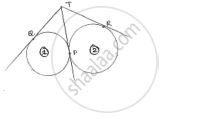
Let the circles be represented by (i) & (ii) respectively
TQ, TP are tangents to (i)
TP, TR are tangents to (ii)
We know that
The tangents drawn from external point to the circle will be equal in length.
For circle (i), TQ = TP …. (i)
For circle (ii), TP = TR …. (ii)
From (i) & (ii) TQ = TR
APPEARS IN
RELATED QUESTIONS
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.


In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
