Advertisements
Advertisements
प्रश्न
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
उत्तर
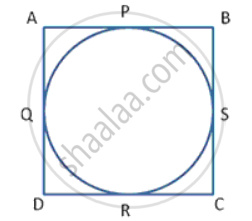
Let the sides of parallelogram ABCD touch the circle at points P, Q, R and S.
AP = AS - (1)
PB = BQ - {2} {Length of tangents drawn from an external point to a circle a equal)
DR = DS - {3}
RC = CQ - (4)
Adding (1), {2}, {3} and (4)
AP + PB + DR + RC = AS + BQ + DS + CQ
AB + CD = AD + BC
2 AB = 2 BC => AB = BC {Opposite sides of a parallelogram are equal)
:. AB = BC = CD = DA,
Hence , ABCD is a rhombus.
APPEARS IN
संबंधित प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

Use the figure given below to fill in the blank:
R is the _______ of the circle.

Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Draw circle with the radii given below.
3 cm
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
