Advertisements
Advertisements
प्रश्न
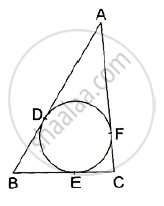
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

उत्तर

Here, D, E and F are the points of contact of the circle with the sides BC, AB and AC, respectively.
OD = OE = OF = 4 cm (Radii of the circle)
We know that the lengths of tangents drawn from an external point to a circle are equal.
∴ BD = BE = 8 cm
CD = CF = 6 cm
AE = AF = x cm (say)
So, BC = BD + CD = 8 cm + 6 cm = 14 cm
AB = AE + BE = x cm + 8 cm = (x + 8) cm
AC = AF + FC = x cm + 6 cm = (x + 6) cm
Also, the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OD ⊥ BC, OE ⊥ AB and OF ⊥ AC
Now,
ar(∆OBC) + ar(∆OAB) + ar(∆OCA) = ar(∆ABC)
\[\therefore \frac{1}{2} \times BC \times OD + \frac{1}{2} \times AB \times OE + \frac{1}{2} \times AC \times OF = 84 {cm}^2 \]
\[ \Rightarrow \frac{1}{2} \times 14 \times 4 + \frac{1}{2} \times \left( x + 8 \right) \times 4 + \frac{1}{2} \times \left( x + 6 \right) \times 4 = 84\]
\[ \Rightarrow 28 + 2x + 16 + 2x + 12 = 84\]
\[ \Rightarrow 4x + 56 = 84\]
\[\Rightarrow 4x = 84 - 56 = 28\]
\[ \Rightarrow x = 7\]
∴ AB = (x + 8) cm = (7 + 8) cm = 15 cm
AC = (x + 6) cm = (7 + 6) cm = 13 cm
Hence, the lengths of sides AB and AC are 15 cm and 13 cm, respectively.
संबंधित प्रश्न
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
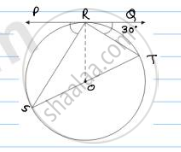
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

Number of circles that can be drawn through three non-collinear points is
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
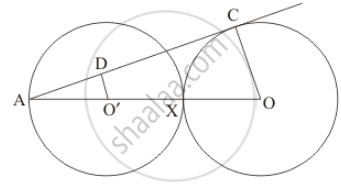
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
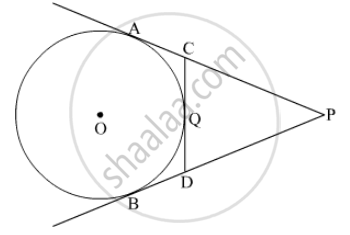
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

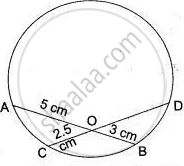
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
The diameter of a circle is 12.6 cm. State, the length of its radius.
Draw circle with the radii given below.
3 cm
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?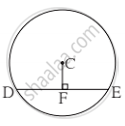
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify a point in the exterior.

Say true or false:
Two diameters of a circle will necessarily intersect.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
