Advertisements
Advertisements
प्रश्न
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
उत्तर
Given AD = 23 cm
AB = 29 cm
∠B = 90°
DS = 5cm
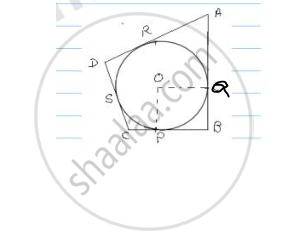
From fig in quadrilateral POQB
∠OPB = ∠OQB = 90° = ∠B = ∠POQ
and PO = OQ. ∴ POQB is a square PB = BQ = r
We know that
Tangents drawn from external point to circle are equal in length.
We know that
Tangents drawn from external point to circle are equal in length.
From A, AR = AQ …. (i)
From B, PB = QB …. (ii)
From C, PC = CS …. (iii)
From D, DR = DS …. (iv)
(i) + (ii) + (iv) ⇒ AR + DB + DR = AQ + QB + DS
⇒ (AR + DR) + r = (AQ + QB) + DS
AD + r = AB + DS
⇒ 23 + r = 29 + 5
⇒ r = 34 – 23 = 11 cm
∴ radius = 11 cm
APPEARS IN
संबंधित प्रश्न
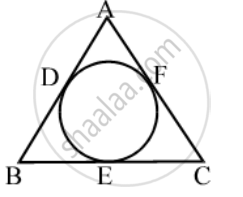
In Fig., if AB = AC, prove that BE = EC
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
Write True or False. Give reason for your answer.
A circle is a plane figure.
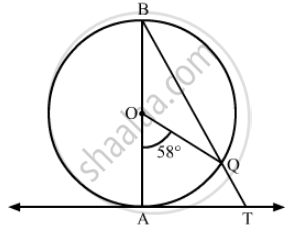
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.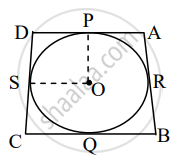
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______