Advertisements
Advertisements
प्रश्न
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

उत्तर
AB = 10 cm,
BC = 8 cm and
AC = 6 cm
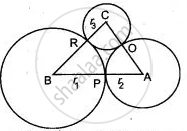
Let the radii of three circle be r1, r2 and r3 ...(Shown in fig.)
r1 + r2 = 10 = AB ....(1)
r2 + r3 = 6 = AC ....(2)
r3 + r1 = 8 = BC .....(3)
Adding (1), (2) and (3), we get
2 (r1 + r2 + r3 ) = 10 + 6 + 8 = 24
r1 + r2 + r3 = 12 .....(4)
Subtract (4) and (1) ⇒ r3 = 12 - 10 = 2 cm
Subtract (4) and (2) ⇒ r1 = 12 - 6 = 6 cm
Subtract (4) and (3) ⇒ r2 = 12 - 8 = 4 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
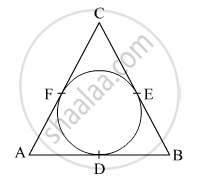
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
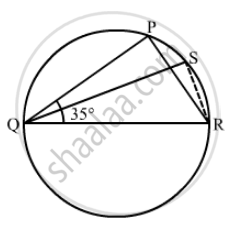
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
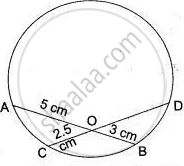
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.