Advertisements
Advertisements
प्रश्न
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
उत्तर
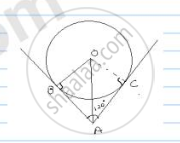
Consider Centre O for given circle
∠BAC = 120°
AB and AC are tangents
From the fig.
In ΔOBA, ∠OBA = 90° [radius perpendicular to tangent at point of contact]
∠OAB = ∠OAC =`1/2`∠𝐵𝐴𝐶 =`1/2`× 120° = 60°
[Line joining Centre to external point from where tangents are drawn bisects angle formed by tangents at that external point1]
In ΔOBA, cos 60° =`(AB)/(OA)`
`1/2=(AB)/(OA)`⇒ 𝑂𝐴 = 2𝐴𝐵
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Find the area of a circle of radius 7 cm.
The radius of a circle of diameter 24 cm is _______
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
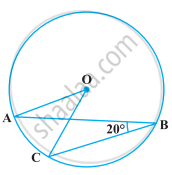
From the figure, identify a diameter.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
