Advertisements
Advertisements
प्रश्न
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
उत्तर
Given: ABCD is a parallelogram where the diagonal BD bisects
parallelogram ABCD at angle B and D
To Prove: ABCD is a rhombus
Proof: Let us draw a parallelogram ABCD where the diagonal BD bisects the parallelogram at an angle B and D.
Construction: Let us join AC as a diagonal of the parallelogram ABCD
Since ABCD is a parallelogram in which diagonal BD bisects ∠B and ∠D
BD bisect ∠B,
∠ABD = ∠CBD = `1/2`∠ABC
BD bisect ∠D,
∠ADB = ∠CDB = `1/2`∠ABC
∴ ∠ABC = ∠ADC ...(Opposite angles of parallelogram are equal)
∴ `1/2`∠ABC = `1/2` ∠ADC
∠ABD = ∠ADB and ∠CBD = ∠CDB
∴ AD = AB and CD = BC
As ABCD is a parallelogram, opposite sides are equal
AB = CD and AD = BC
AB = BC = CD = AD
∴ ABCD is a rhombus.
APPEARS IN
संबंधित प्रश्न
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 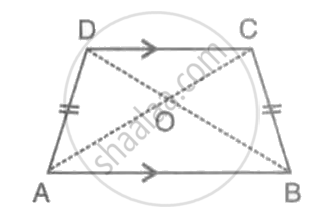
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.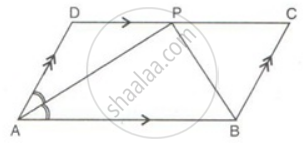
Prove that: ∠APB is a right angle.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.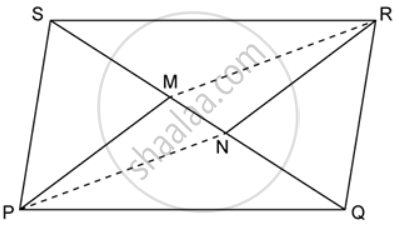
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.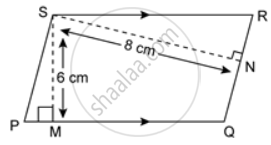
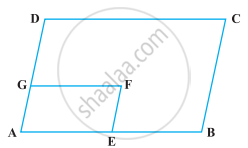
In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
Which of the following statement is correct?
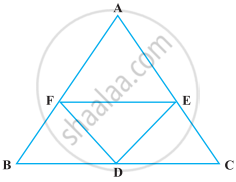
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.