Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.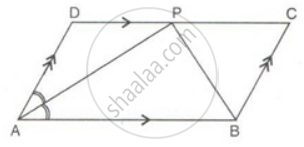
Prove that: ∠APB is a right angle.
उत्तर
∠DAP =∠PAB
∠CBP = ∠PBA
∠DAB + ∠CBA = 180° ...(adjacent angles of || gm are supplementary)
Multipying by `(1)/(2)`
`(1)/(2)∠"DAB" + (1)/(1)∠"CBA" = (1)/(2) xx 180°`
∠PAB + ∠PBA = 90°
In ΔAPB,
∠PAB + ∠PBA + ∠APB = 180°
90° + ∠APB = 180°
∠APB = 90°
Therefore, ∠APB is a right angle.
APPEARS IN
संबंधित प्रश्न
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
Prove that the bisectors of opposite angles of a parallelogram are parallel.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.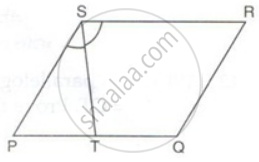
Prove that: ∠RTS = 90°
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.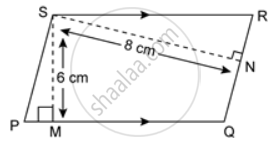
Which of the following statement is correct?
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?