Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.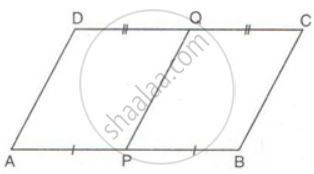
उत्तर
In quandrilateral APCQ,
AP || QC ...(since AB || CD)
AP = `(1)/(2)"AB"` ...(given)
CQ = `(1)/(2)"CD"` ...(given)
But AB = CD
⇒ AP = CQ
Therefore, APCQ is a parallelogram.
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.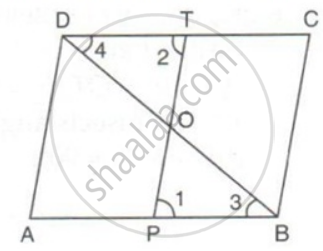
PQRS is a parallelogram. PQ is produced to T so that PQ = QT. Prove that PQ = QT. Prove that ST bisects QR.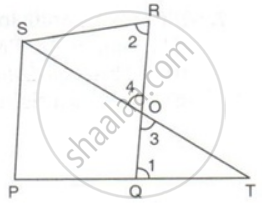
ABCD is a rectangle with ∠ADB = 55°, calculate ∠ABD.
ABCD is a quadrilateral P, Q, R and S are the mid-points of AB, BC, CD and AD. Prove that PQRS is a parallelogram.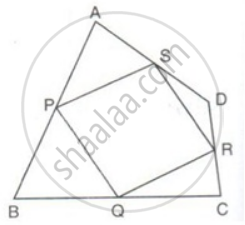
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
MN bisects QS.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
Prove that the diagonals of a kite intersect each other at right angles.
The medians QM and RN of ΔPQR intersect at O. Prove that: area of ΔROQ = area of quadrilateral PMON.
