Advertisements
Advertisements
प्रश्न
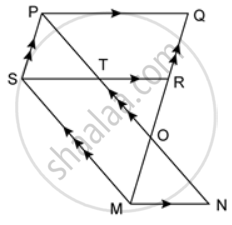
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
MN bisects QS.
उत्तर
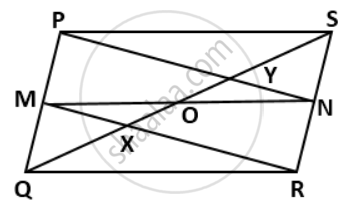
M and N are the mid-points of PQ and RS respectively.
⇒ MN || QR
Let MN intersect QS at point O.
We know that the segment drawn through the mid-point of one side of a triangle and parallel to the other sides bisects the third side.
In ΔSRQ, N is the mid-point of RS and ON || QR
∴ O is the mid-point of SQ
⇒ OQ = OS ....(iii)
⇒ ON bisects QS
⇒ MN bisects QS.
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.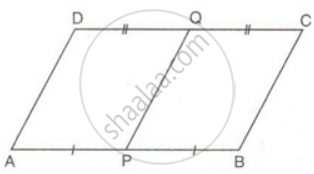
PQRS is a parallelogram. PQ is produced to T so that PQ = QT. Prove that PQ = QT. Prove that ST bisects QR.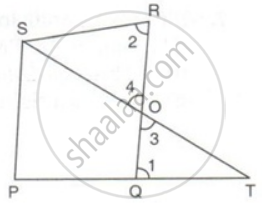
P is a point on side KN of a parallelogram KLMN such that KP : PN is 1 : 2. Q is a point on side LM such that LQ : MQ is 2 : 1. Prove that KQMP is a parallelogram.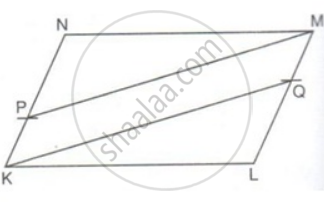
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
ABCD is a trapezium in which side AB is parallel to side DC. P is the mid-point of side AD. IF Q is a point on the Side BC such that the segment PQ is parallel to DC, prove that PQ = `(1)/(2)("AB" + "DC")`.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
Prove that the diagonals of a kite intersect each other at right angles.
Prove that the diagonals of a parallelogram divide it into four triangles of equal area.
PQRS is a parallelogram and O is any point in its interior. Prove that: area(ΔPOQ) + area(ΔROS) - area(ΔQOR) + area(ΔSOP) = `(1)/(2)`area(|| gm PQRS)
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).