Advertisements
Advertisements
प्रश्न
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
उत्तर
The area of a square plot with side 80m
= 802
= 6400m2
Let the width of the rectangular plot = b
The area of a rectangle with length l and breadth b = A = l x b
The area of a rectangle wit length 160 and breadth b = A = 160 x b = 6400
⇒ b = `(6400)/(160)`
= 40m
The perimeter of a rectangle with length l and breadth b = P = 2(l + b)
The perimeter of a rectangle with length 160m and breadth 40m
= P
= 2(160 + 40)
= 2(200)
= 400m
The cost of fencing at the rate of Rs.7.50per m
= 400 x 7.50
= Rs.3000.
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.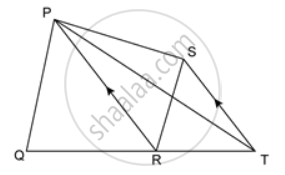
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.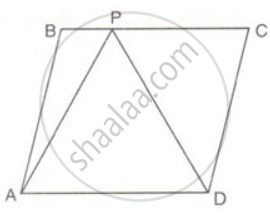
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.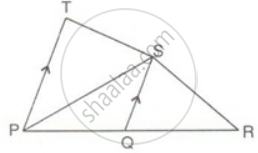
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure: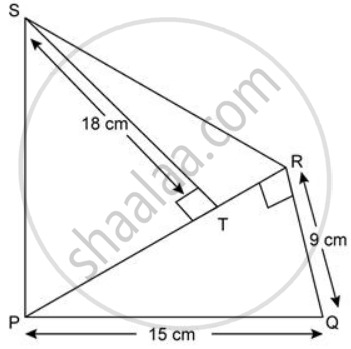
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
A lawn in the shape of a rectangle is to be developed in front of a Marriage Hall. The length and breadth of the lawn are 44m and 32m. A space of 2m is left on the two shoulder sides and one longer side for flower and in the remaining area grass is laid. Calculate the area of the flower space and the area on which grass is laid.
The opposite sides of a trapezium are parallel.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Examine whether the following is a polygon. If it is not, say why?

