Advertisements
Advertisements
प्रश्न
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
उत्तर
Diagonal of a square = `5sqrt(2)"cm"`
⇒ Side of a square x `sqrt(2) = 5sqrt(2)`
⇒ Side pf a square = 5cm
Thus, w have
Perimeter of a square
= 4 x Side
= 4 x 5
= 20cm
Area of a square
= (Side)2
= (5)2
= 25cm2.
APPEARS IN
संबंधित प्रश्न
Show that the diagonals of a square are equal and bisect each other at right angles.
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.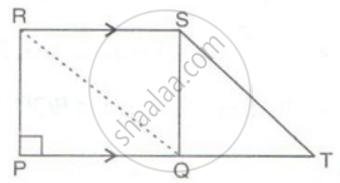
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
In the given figure, ABC is a triangle and AD is the median.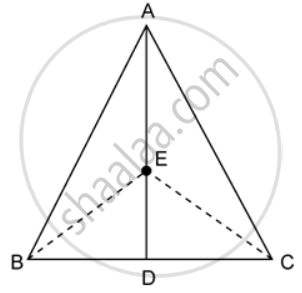
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
Find the area of each of the following figure:
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
Each angle of a rectangle is a right angle.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reason for the following :
Square is also a parallelogram.
