Advertisements
Advertisements
प्रश्न
Show that the diagonals of a square are equal and bisect each other at right angles.
उत्तर
Let ABCD be a square such that its diagonals AC and BD intersect at O.
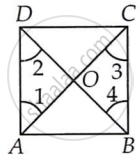
(i) To prove that the diagonals are equal, we need to prove AC = BD.
In ΔABC and ΔBAD, we have
AB = BA ...[Common]
BC = AD ...[Sides of a square ABCD]
∠ABC = ∠BAD ...[Each angle is 90°]
∴ ΔABC ≅ ΔBAD ...[By SAS congruency]
⇒ AC = BD ...[By CPCT] ...(1)
(ii) AD || BC and AC is a transversal. ...[∵ A square is a parallelogram]
∴ ∠1 = ∠3 ...[Alternate interior angles are equal]
Similarly, ∠2 = ∠4
Now, in ΔOAD and ΔOCB, we have
AD = CB ...[Sides of a square ABCD]
∠1 = ∠3 ...[Proved]
∠2 = ∠4 ...[Proved]
∴ ΔOAD ≅ ΔOCB ...[By ASA congruency]
⇒ OA = OC and OD = OB ...[By CPCT] ...(2)
i.e., the diagonals AC and BD bisect each other at O.
(iii) In ΔOBA and ΔODA, we have
OB = OD ...[Proved]
BA = DA ...[Sides of a square ABCD]
OA = OA ...[Common]
∴ ΔOBA ≅ ΔODA ...[By SSS congruency]
⇒ ∠AOB = ∠AOD ...[By CPCT] ...(3)
∵ ∠AOB and ∠AOD form a linear pair
∴ ∠AOB + ∠AOD = 180°
∴ ∠AOB = ∠AOD = 90° ...[By (3)]
AC ⊥ BD ...(4)
From (1), (2) and (4), we get AC and BD are equal and bisect each other at right angles.
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.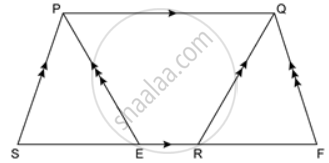
Find the area of each of the following figure: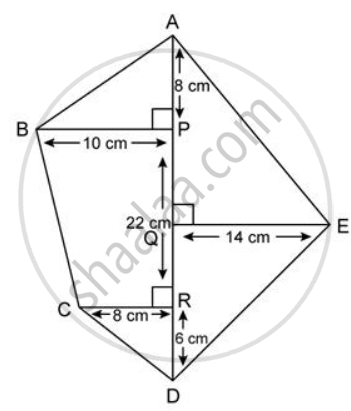
Find the area of each of the following figure: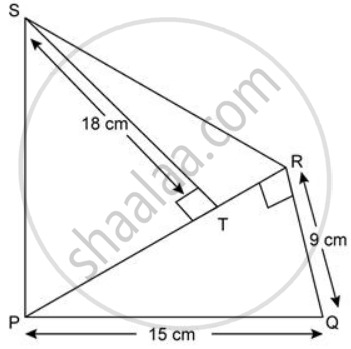
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
Each angle of a rectangle is a right angle.
Examine whether the following is a polygon. If it is not, say why?

