Advertisements
Advertisements
प्रश्न
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
उत्तर
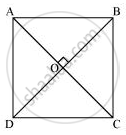
Let us consider a quadrilateral ABCD in which the diagonals AC and BD intersect each other at O. It is given that the diagonals of ABCD are equal and bisect each other at right angles. Therefore, AC = BD, OA = OC, OB = OD, and ∠AOB = ∠BOC = ∠COD = ∠AOD = 90º. To prove ABCD is a square, we have to prove that ABCD is a parallelogram, AB = BC = CD = AD, and one of its interior angles is 90º.
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
OB = OD (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite angles)
∴ ΔAOB ≅ ΔCOD (SAS congruence rule)
∴ AB = CD (By CPCT) ... (1)
And, ∠OAB = ∠OCD (By CPCT)
However, these are alternate interior angles for line AB and CD and alternate interior angles are equal to each other only when the two lines are parallel.
∴ AB || CD ... (2)
From equations (1) and (2), we obtain
ABCD is a parallelogram.
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Given that each is 90º)
OD = OD (Common)
∴ ΔAOD ≅ ΔCOD (SAS congruence rule)
∴ AD = DC ... (3)
However, AD = BC and AB = CD (Opposite sides of parallelogram ABCD)
∴ AB = BC = CD = DA
Therefore, all the sides of quadrilateral ABCD are equal to each other.
In ΔADC and ΔBCD,
AD = BC (Already proved)
AC = BD (Given)
DC = CD (Common)
∴ ΔADC ≅ ΔBCD (SSS Congruence rule)
∴ ∠ADC = ∠BCD (By CPCT)
However, ∠ADC + ∠BCD = 180° (Co-interior angles)
⇒ ∠ADC + ∠ADC = 180°
⇒ 2∠ADC = 180°
⇒ ∠ADC = 90°
One of the interior angles of quadrilateral ABCD is a right angle.
Thus, we have obtained that ABCD is a parallelogram, AB = BC = CD = AD and one of its interior angles is 90º. Therefore, ABCD is a square.
APPEARS IN
संबंधित प्रश्न
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
The following statement are true and false .
In a parallelogram, the diagonals intersect each other at right angles .
The following statement are true and false .
In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram.
The following statement are true and false .
If three sides of a quadrilateral are equal, it is a parallelogram .
Complete the following statement by means of one of those given in brackets against each:
If one angle of a parallelogram is a right angle, then it is necessarily a .................
The bisectors of any two adjacent angles of a parallelogram intersect at
The bisectors of the angle of a parallelogram enclose a
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a
If one angle of a parallelogram is 24° less than twice the smallest angle, then the measure of the largest angle of the parallelogram is
Diagonals of a quadrilateral ABCD bisect each other. If ∠A= 45°, then ∠B =
