Advertisements
Advertisements
Question
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution
Let ABCD be a square such that its diagonals AC and BD intersect at O.
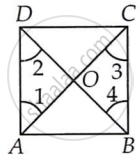
(i) To prove that the diagonals are equal, we need to prove AC = BD.
In ΔABC and ΔBAD, we have
AB = BA ...[Common]
BC = AD ...[Sides of a square ABCD]
∠ABC = ∠BAD ...[Each angle is 90°]
∴ ΔABC ≅ ΔBAD ...[By SAS congruency]
⇒ AC = BD ...[By CPCT] ...(1)
(ii) AD || BC and AC is a transversal. ...[∵ A square is a parallelogram]
∴ ∠1 = ∠3 ...[Alternate interior angles are equal]
Similarly, ∠2 = ∠4
Now, in ΔOAD and ΔOCB, we have
AD = CB ...[Sides of a square ABCD]
∠1 = ∠3 ...[Proved]
∠2 = ∠4 ...[Proved]
∴ ΔOAD ≅ ΔOCB ...[By ASA congruency]
⇒ OA = OC and OD = OB ...[By CPCT] ...(2)
i.e., the diagonals AC and BD bisect each other at O.
(iii) In ΔOBA and ΔODA, we have
OB = OD ...[Proved]
BA = DA ...[Sides of a square ABCD]
OA = OA ...[Common]
∴ ΔOBA ≅ ΔODA ...[By SSS congruency]
⇒ ∠AOB = ∠AOD ...[By CPCT] ...(3)
∵ ∠AOB and ∠AOD form a linear pair
∴ ∠AOB + ∠AOD = 180°
∴ ∠AOB = ∠AOD = 90° ...[By (3)]
AC ⊥ BD ...(4)
From (1), (2) and (4), we get AC and BD are equal and bisect each other at right angles.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.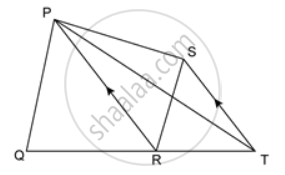
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
The opposite sides of a rectangle are equal in length.
The opposite sides of a trapezium are parallel.
