Advertisements
Advertisements
Question
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Solution
The area of a rectangle with length l and breadth b = A = l x b
∴ The area of the rectangular plot with length 160m and breadth 40m
= A
= 160 x 40
= area of the square garden
We know,
The area of a square with side s = s2
∴ s2 = 160 x 40
⇒ s = `sqrt(160 xx 40)`
= `sqrt(16 xx 4 xx 100)`
= 4 x 2 x 10
= 80m
The perimeter of a square with side
= P
= 4s
∴ The perimeter of a square with side 80
= 4 x 80
= 320m
The cost of fencing at the rate of Rs.12per m
= 320 x 12
= Rs.3840.
APPEARS IN
RELATED QUESTIONS
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the following figures, ABCD is a parallelogram.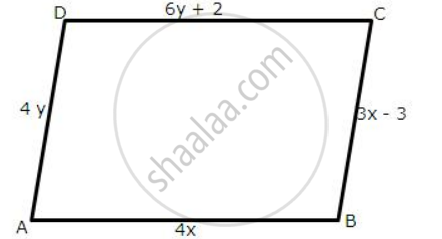
find the values of x and y.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.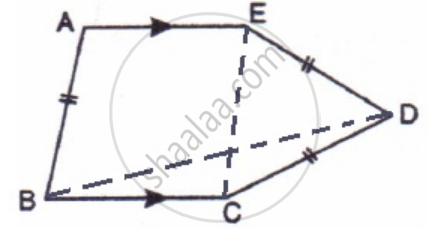
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.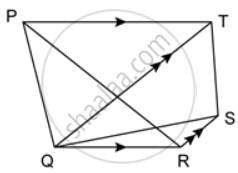
*Question modified
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
