Advertisements
Advertisements
Question
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.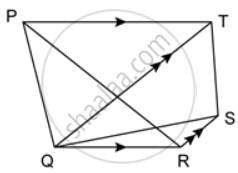
*Question modified
Solution
Joining TR, we get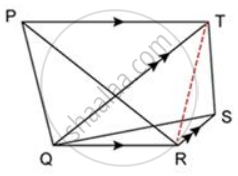
ΔPQR and ΔQTR are on the same base QR and between the same parallel lines QR and PT.
∴ A(ΔPQR) = A(ΔQTR) ....(i)
ΔQTR and ΔTQS are on the same base QT and between the same parallel lines QT and RS.
∴ A(ΔQRT) = A(ΔTQS) ....(ii)
From (i) and (ii), we get
A(ΔPQR) = A(ΔTQS).
APPEARS IN
RELATED QUESTIONS
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.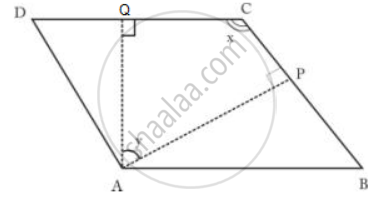
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the following figures, ABCD is a parallelogram.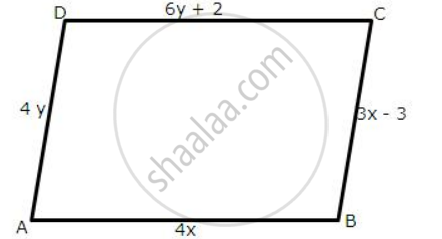
find the values of x and y.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.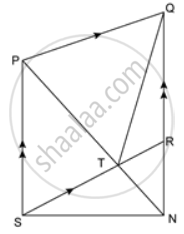
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
In the given figure, ABC is a triangle and AD is the median.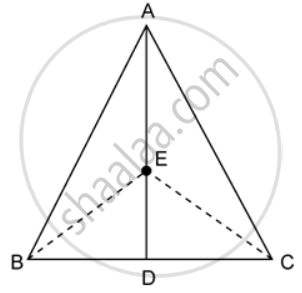
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
All the sides of a parallelogram are of equal length.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?
Name polygon.
Make two more examples of this.
