Advertisements
Advertisements
Question
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Solution
In a square, all the interior angles are of 90° and all the sides are of the same length. Therefore, a square is a regular quadrilateral.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
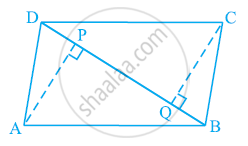
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
Find the area of each of the following figure: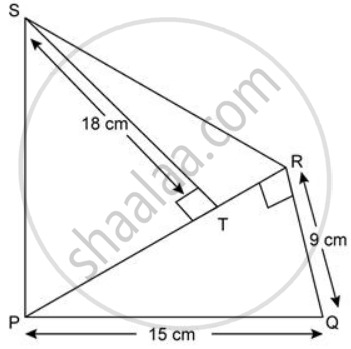
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
Give reasons for the following :
A square can be thought of as a special rhombus.
