Advertisements
Advertisements
Question
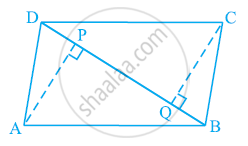
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
Solution
i. In ΔAPB and ΔCQD,
∠APB = ∠CQD ...(Each 90°)
AB = CD ...(Opposite sides of parallelogram ABCD)
∠ABP = ∠CDQ ...(Alternate interior angles for AB || CD)
∴ ΔAPB ≅ ΔCQD ...(By AAS congruency)
ii. By using the above result
ΔAPB ≅ ΔCQD, we obtain
AP = CQ ...(By CPCT)
APPEARS IN
RELATED QUESTIONS
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.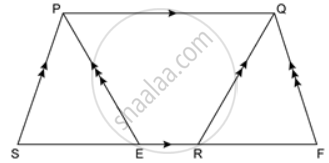
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.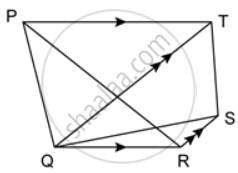
*Question modified
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Square is also a parallelogram.
Name polygon.

Make two more examples of this.
Name polygon.

Make two more examples of this.
