Advertisements
Advertisements
प्रश्न
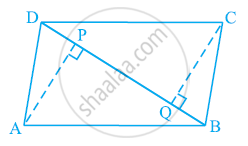
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
उत्तर
i. In ΔAPB and ΔCQD,
∠APB = ∠CQD ...(Each 90°)
AB = CD ...(Opposite sides of parallelogram ABCD)
∠ABP = ∠CDQ ...(Alternate interior angles for AB || CD)
∴ ΔAPB ≅ ΔCQD ...(By AAS congruency)
ii. By using the above result
ΔAPB ≅ ΔCQD, we obtain
AP = CQ ...(By CPCT)
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN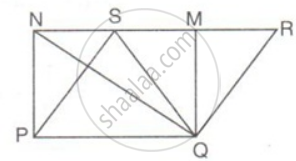
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.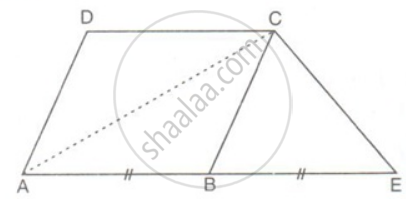
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure: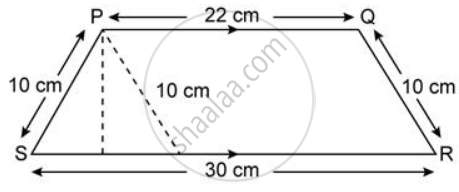
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Each angle of a rectangle is a right angle.
The diagonals of a square are perpendicular to one another.
Give reason for the following :
Square is also a parallelogram.
