Advertisements
Advertisements
Question
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.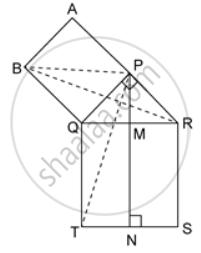
Solution
∠BQR = ∠BQP + ∠PQR
⇒ ∠BQR = 90° + ∠PQR
∠PQT = ∠TQR + ∠PQR
⇒ ∠PQT = 90° + ∠PQR ....(i)
⇒ ∠BQR = ∠PQT
(a) In ΔQRB and ΔPQT,
BQ = PQ ....(sides of a square PABQ)
QR = QT ....(sides of a square QRST)
∠BQR = ∠PQT ...[From (i)]
∴ ΔQRB ≅ ΔPQT ...(by SAS congruence criterion)
⇒ A(ΔBQR) = A(ΔPQT) ....(ii)
(b) ΔPQT and rect. QTNM are on the same base QT
and between the same parallel lines QT and PN.
∴ A(ΔPQT) = `(1)/(2)"A"("rect. QTNM")`
⇒ A(rect. QTMN) = x A(ΔPQT)
⇒ A(rect. QTMN) = x ar(ΔBQR) [From (ii)]....(iii)
ΔBQR and sq. PABQ are on the same base BQ
and between the same parallel lines BQ and AR.
∴ 2 x A(ΔBQR) = A(sq. PABQ) ....(iv)
From (i) and (iv),
A(sq. PABQ) = A(rect. QTNM)
APPEARS IN
RELATED QUESTIONS
All squares are rhombuses and also rectangles.
All squares are not parallelograms.
Explain how a square is a parallelogram
Explain how a square is a rectangle
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ;
prove that AP and DQ are perpendicular to each other.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
PQRS is a square whose diagonals PR and QS intersect at O.M is a point on QR such that OQ = MQ. Find the measures of ∠MOR and ∠QSR.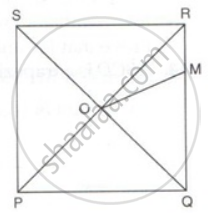
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.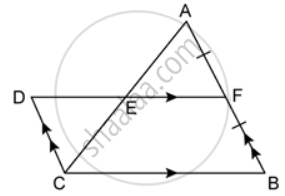
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
