Advertisements
Advertisements
Question
PQRS is a square whose diagonals PR and QS intersect at O.M is a point on QR such that OQ = MQ. Find the measures of ∠MOR and ∠QSR.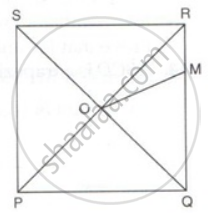
Solution
In ΔQOM,
∠OQM = 45° ...(In square diagonals make 45° with the sides)
OQ = MQ
⇒ ∠QOM = ∠QMO (i) ...(equal sides have equal angles opposite to them)
∠QOM + ∠QMO + ∠OQM = 180°
∠QOM + ∠QOM + 45° = 180°
2∠QOM = 180° - 45°
∠QOM = 67.5°
In ΔQOR,
∠QOR = 90° ...(diagonals bisect at right angles)
∠QOM + ∠MOR = 90°
67.5° + ∠MOR = 90°
∠MOR = 22.5°
In ΔROS,
∠OSR = 45° ...(In square diagonals make 45° with the sides)
⇒ ∠QSR = 45°.
APPEARS IN
RELATED QUESTIONS
All rectangles are squares
All squares are rhombuses and also rectangles.
All squares are not parallelograms.
Explain how a square is a quadrilateral
Prove that the bisectors of the interior angles of a rectangle form a square.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ;
prove that AP and DQ are perpendicular to each other.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QS = 9x – 8. Find QS
Prove that the quadrilateral formed by joining the mid-points of a square is also a square.
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
