Advertisements
Advertisements
Question
In the given figure, ABC is a triangle and AD is the median.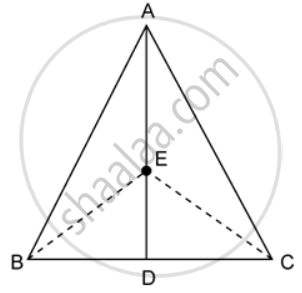
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
Solution
AD is the median of ΔABC.
Therefore it will divide ΔABC into two triangles of equal areas.
∴ Area(ΔABD) = Area(ΔACD) ….(i)
Similarly, ED is the median of ΔEBC.
∴ Area(ΔEBD) = Area(ΔECD) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔABD) - Area(ΔEBD) = Area(ΔACD) - Area(ΔECD)
⇒ Area(ΔABE) = Area(ΔACE) ….(iii)
Since E is the mid-point of median AD,
AE = ED
Now,
ΔABE and ΔBED have equal bases and a common vertex B.
∴ Area(ΔABE) = Area(ΔBED) ….(iv)
From (i), (ii), (iii) and (iv), we get
Area(ΔABE) = A(ΔBED) = Area(ΔACE) = Area(ΔEDC) ….(v)
Now,
Area(ΔABC) = Area(ΔABE) + A(ΔBED) + Area(ΔACE) + Area(ΔEDC)
= 4 × Area(ΔABE). [From (v)]
APPEARS IN
RELATED QUESTIONS
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.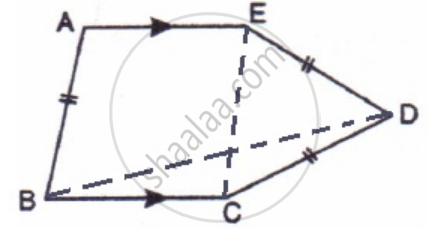
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.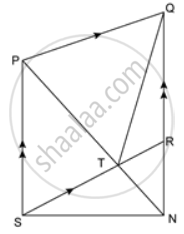
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
Find the area of each of the following figure: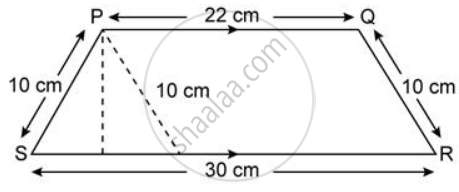
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
A rectangular floor 45 in long and 12 m broad is to be paved exactly with square tiles, of side 60 cm. Find the total number of tiles required to pave it.
If a carpet is laid on the floor such as a space of 50 cm exists between its edges and the edges of the floor, find what fraction of the floor is uncovered.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
Give reasons for the following :
A square can be thought of as a special rhombus.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
