Advertisements
Advertisements
प्रश्न
In the given figure, ABC is a triangle and AD is the median.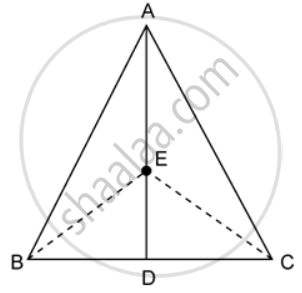
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
उत्तर
AD is the median of ΔABC.
Therefore it will divide ΔABC into two triangles of equal areas.
∴ Area(ΔABD) = Area(ΔACD) ….(i)
Similarly, ED is the median of ΔEBC.
∴ Area(ΔEBD) = Area(ΔECD) ….(ii)
Subtracting equation (ii) from (i), we have
Area(ΔABD) - Area(ΔEBD) = Area(ΔACD) - Area(ΔECD)
⇒ Area(ΔABE) = Area(ΔACE) ….(iii)
Since E is the mid-point of median AD,
AE = ED
Now,
ΔABE and ΔBED have equal bases and a common vertex B.
∴ Area(ΔABE) = Area(ΔBED) ….(iv)
From (i), (ii), (iii) and (iv), we get
Area(ΔABE) = A(ΔBED) = Area(ΔACE) = Area(ΔEDC) ….(v)
Now,
Area(ΔABC) = Area(ΔABE) + A(ΔBED) + Area(ΔACE) + Area(ΔEDC)
= 4 × Area(ΔABE). [From (v)]
APPEARS IN
संबंधित प्रश्न
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show that the diagonals of a square are equal and bisect each other at right angles.
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.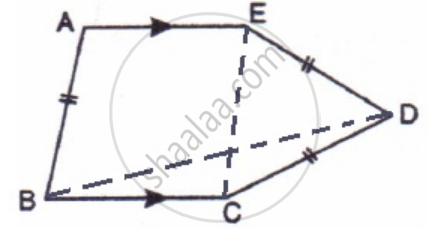
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
Find the area of each of the following figure: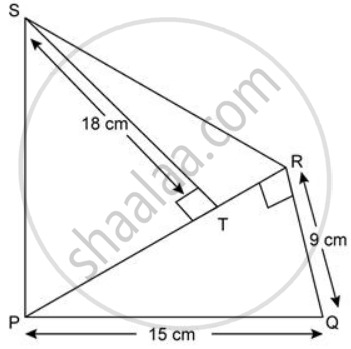
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
The opposite sides of a rectangle are equal in length.
All the sides of a rhombus are of equal length.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
