Advertisements
Advertisements
प्रश्न
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
उत्तर
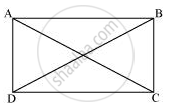
Let ABCD be a parallelogram. To show that ABCD is a rectangle, we must prove that one of its interior angles is 90°.
In ΔABC and ΔDCB,
AB = DC ...(Opposite sides of a parallelogram are equal)
BC = BC ...(Common)
AC = DB ...(Given)
∴ ΔABC ≅ ΔDCB ...(By SSS Congruence rule)
⇒ ∠ABC = ∠DCB
It is known that the sum of the measures of angles on the same side of transversal is 180°.
∠ABC + ∠DCB = 180° ...(AB || CD)
⇒ ∠ABC + ∠ABC = 180°
⇒ 2∠ABC = 180°
⇒ ∠ABC = 90°
Since ABCD is a parallelogram and one of its interior angles is 90°, ABCD is a rectangle.
APPEARS IN
संबंधित प्रश्न
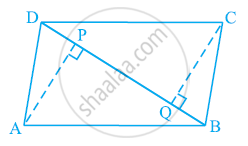
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN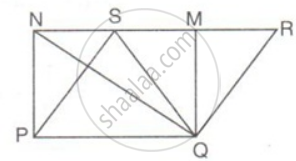
Find the area of each of the following figure:
Find the area of each of the following figure: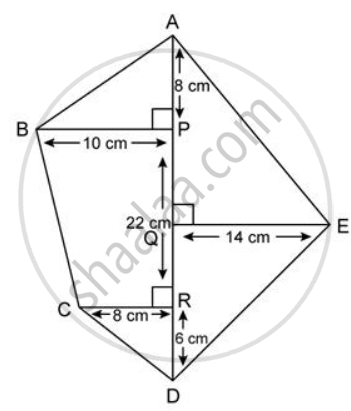
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Name polygon.

Make two more examples of this.
