Advertisements
Advertisements
प्रश्न
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
उत्तर
The perimeter of a square with side s = p = 4s
∴ Here, the perimeter of the square are 128cm and 96cm
∴ the sides of the two squares are 32cm and 24cm
We know, The area of a square with side s = s2
∴ the areas of the two squares are = 32cm2 = 1024cm2 and 24cm2 = 576cm2
∴ the combined area
= area of the new square
= 1024cm2 + 576cm2
= 1600cm2
the side of the square
= `sqrt(1600)`
= 40cm
The perimeter of a square with side 40
= 4 x 40
= 160cm
The sides and diagonal of a square from a right triangle as each angle of a square is a right angle.
Diagonal is the side opposite to the right angle, therefore it is the hypotenuse
Here, diagonal of the square
= `sqrt(40^2 + 40^2)`
= `40sqrt(2)`
= 40(1.414)
= 56.57cm.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
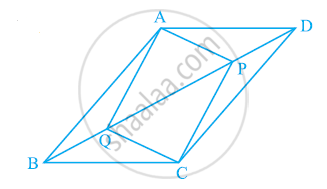
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
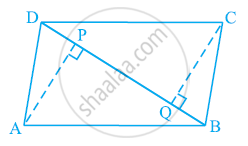
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
Every rhombus is a parallelogram.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.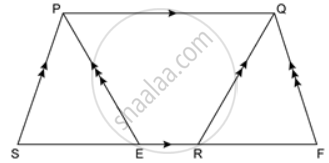
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.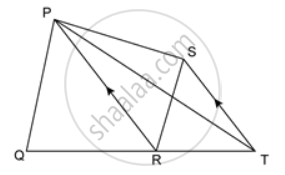
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.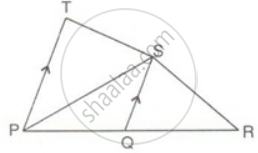
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
The opposite sides of a trapezium are parallel.
Give reasons for the following :
A square can be thought of as a special rhombus.
Give reason for the following :
Square is also a parallelogram.
Examine whether the following is a polygon. If it is not, say why?

