Advertisements
Advertisements
प्रश्न
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.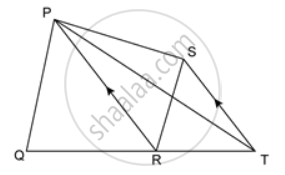
उत्तर
We have,
A(ΔPSR) = A(ΔPTR)
(Triangle on the same base PR and between the same parallel lines PR and ST)
Adding A(ΔPQR) on both sides, we get
A(ΔPSR) + A(ΔPQR) = A(ΔPTR) + A(ΔPQR)
⇒ A(Quadrilateral PQRS) = A(ΔPQT).
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
State, 'true' or 'false'
The diagonals of a rectangle bisect each other.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
In the following figures, ABCD is a parallelogram.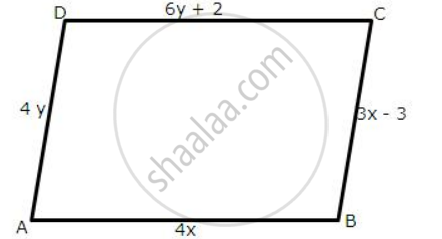
find the values of x and y.
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
Find the area of each of the following figure: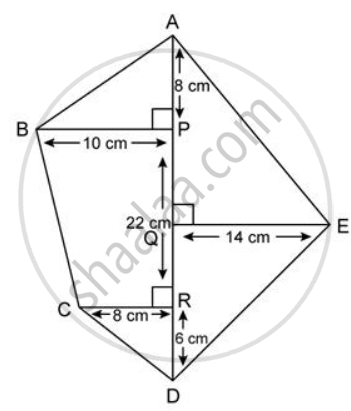
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
The diagonals of a square are perpendicular to one another.
Give reason for the following :
A square can be thought of as a special rectangle.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?

Name polygon.
Make two more examples of this.
