Advertisements
Advertisements
प्रश्न
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.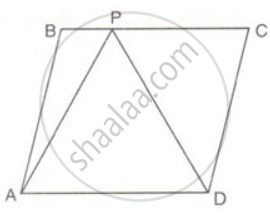
उत्तर
ar(ΔAPD) = `(sqrt(3)"s"^2)/(4)`
ar(ΔAPD) = `(sqrt(3) xx 8^2)/(4)`
ar(ΔAPD) = `(sqrt(3) xx 64)/(4)`
ar(ΔAPD) = `sqrt(3) xx 16 = 16sqrt(3)"cm"^2`
ar(ΔAPD) = `(1)/(2)` x ar(parallelogram ABCD)
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
⇒ ar(parallelogram ABCD) = 2 x ar(ΔAPD)
⇒ ar(parallelogram ABCD) = 2 x `16sqrt(3)"cm"^2`
⇒ ar(parallelogram ABCD) = `32sqrt(3)"cm"^2`.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.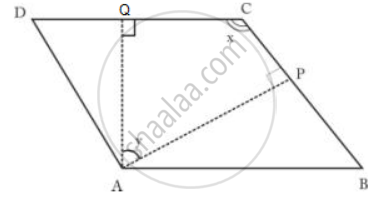
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
In the following figures, ABCD is a parallelogram.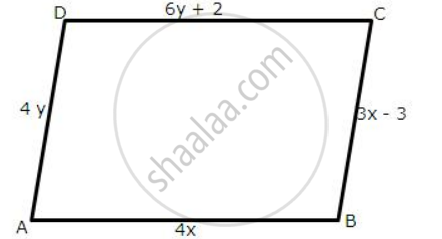
find the values of x and y.
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
Find the area of each of the following figure: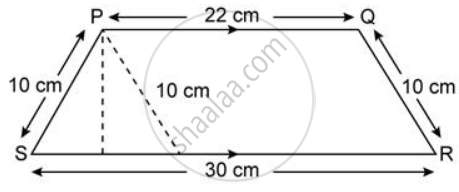
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
All the sides of a rhombus are of equal length.
Give reasons for the following :
A square can be thought of as a special rhombus.
