Advertisements
Advertisements
प्रश्न
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN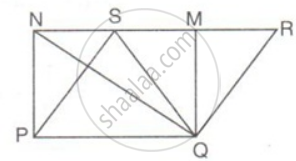
उत्तर
(i) Area of a rectangle and area of a parallelogram on the same base is equal.
Here,
For rectangle PQMN, base = PQ
For parallelogram PQRS, base = PQ
Therefore, Area of rectangle PQMN = Area of parallelogram PQRS
Area of rectangle PQMN = 84cm2
(ii) ar(ΔPQS) = `(1)/(2)` x ar(parallelogram PQRS)
ar(ΔPQS) = `(1)/(2) xx 84"cm"^2`
ar(ΔPQS) = 42cm2
(iii) ar(ΔPQN) = `(1)/(2)` x ar(rectangle PQMN)
ar(ΔPQN) = `(1)/(2) xx 84"cm"^2`
ar(ΔPQN) = 42cm2.
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.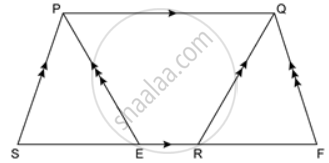
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.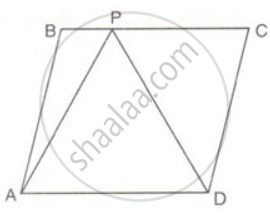
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
In the given figure, ABC is a triangle and AD is the median.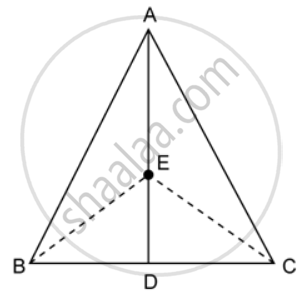
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the area of each of the following figure: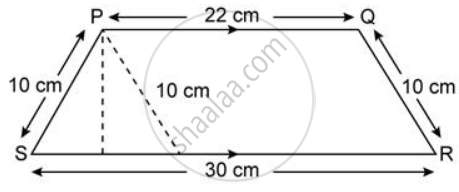
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
The perimeter of a square is 128cm and that of another is 96cm. Find the perimeter and the diagonal of a square whose area is equal to the sum of the areas of these two squares.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
The diagonals of a square are perpendicular to one another.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Name polygon.
Make two more examples of this.
