Advertisements
Advertisements
प्रश्न
Find the area of each of the following figure: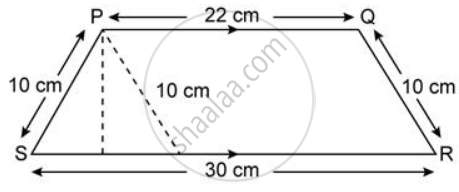
उत्तर
Clearly opposite sides of quadrilateral PQRT are parallel, it is a parallelogram.
ST
= SR - TR
= 30 - 22
= 8cm
In ΔPST,
Let a = PS = 10cm, b = ST = 8cm and C = TP = 10cm
∴ s = `("a" + "b" + "c")/(2)`
= `(10 + 8 + 10)/(2)`
= `(28)/(2)`
= 14cm
Area of ΔPSR
= `sqrt("s"("s"- "a")("s" - "b")("s"-"c")`
= `sqrt(14(14 - 10)(14 - 8)(14 - 10)`
= `sqrt(14 xx 4 xx 6 xx 4)`
= `8sqrt(21)"cm"^2`
If PM is taken height corresponding to base ST,
Area of ΔPST
= `(1)/(2) xx "ST" xx "PM"`
⇒ `8sqrt(21) = (1)/(2) xx 8 xx "PM"`
⇒ PM = `2sqrt(21)"cm"`
∴ Area of given figure
= `(1)/(2) xx("PQ" + "SR") xx "PM"`
= `(1)/(2) xx (22 + 30) xx 2sqrt(21)`
= `(1)/(2) xx 52 xx 2sqrt(21)`
= `52sqrt(21)"cm"^2`.
APPEARS IN
संबंधित प्रश्न
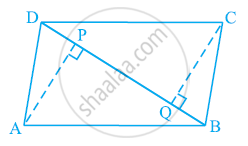
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
The quadrilateral, whose four sides are equal, is a square.
In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.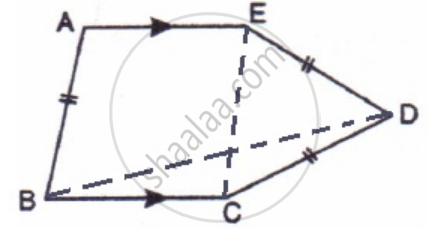
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.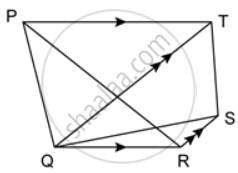
*Question modified
In the given figure, ABC is a triangle and AD is the median.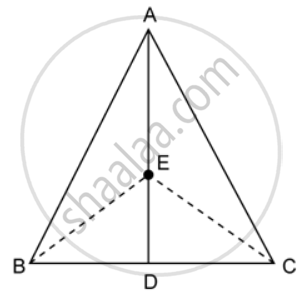
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
In the given figure, ABC is a triangle and AD is the median.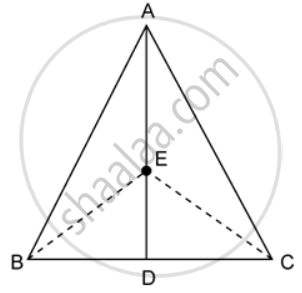
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
Find the area of each of the following figure: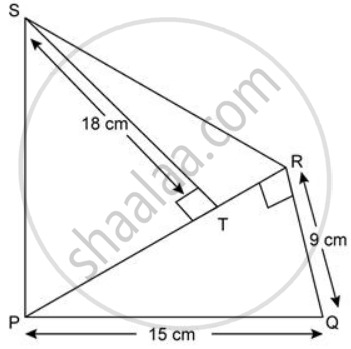
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Each angle of a rectangle is a right angle.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?