Advertisements
Advertisements
प्रश्न
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
उत्तर
Area of a parallelogram with base b and height h is A = b x h
∴ Area of a parallelogram with base 12cm and height 8cm is A = 12 x 8 = 96cm2
Let the length of the adjacent side of the parallelogram = xcm
The height corresponding to it = 16
∴ Area of a parallelogram with base xcm and height 16cm is A = 16x = 96
⇒ x = `(96)/(16)`
= 6cm.
APPEARS IN
संबंधित प्रश्न
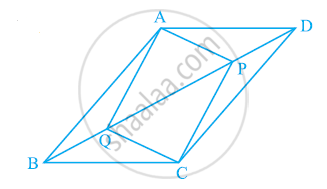
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.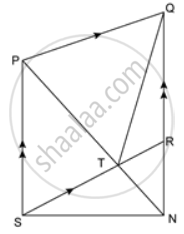
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.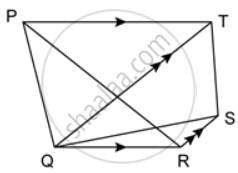
*Question modified
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
Find the area of each of the following figure:
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
All the sides of a rhombus are of equal length.
Give reason for the following :
A square can be thought of as a special rectangle.
