Advertisements
Advertisements
प्रश्न
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
उत्तर
Let the breadth of the rectangle = x m length and of the rectangle = 3x m
The perimeter of a rectangle with length I and breadth b = P = 2(l + b)
∴ The perimeter of a rectangle with length 3x and breadth x = P = 2(3x + x)
= 2(4x) = 8x
⇒ 8x = 1.6km
= 1.6 x 1000m
= 1600m
⇒ x = `(1600)/(8)`
= 200m
⇒ the breadth of the rectangle = 200m length
and of the rectangle = 3(200) = 600m
The area of a rectangle with length l and breadth b = A = l x b
The area of a rectangle with length 600 and breadth 200 = A = 600 x 200 = 120000m2.
APPEARS IN
संबंधित प्रश्न
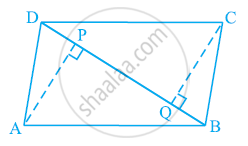
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
Diagonals of a rhombus are equal.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.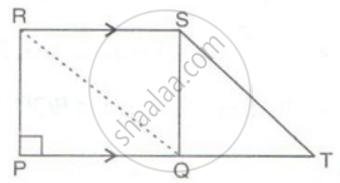
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.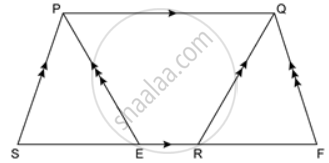
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.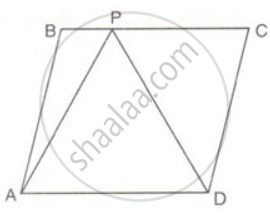
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN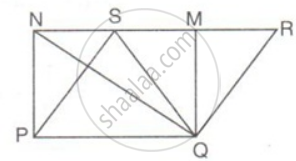
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
In the given figure, ABC is a triangle and AD is the median.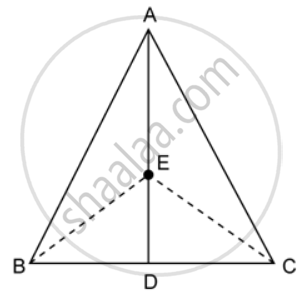
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The opposite sides of a rectangle are equal in length.
Give reason for the following :
Square is also a parallelogram.
Name polygon.
Make two more examples of this.
