Advertisements
Advertisements
प्रश्न
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
उत्तर

(i) Let ∠POC = x°.
We know that,
Each interior angle equals to 90°. Diagonals of square bisect the interior angles.
From figure,
⇒ ∠OCP = ∠OBP = `(90°)/2` = 45°.
We know that,
In a triangle, an exterior angle is equal to sum of two opposite interior angles.
∴ ∠OPB = ∠OCP + ∠POC
⇒ ∠OPB = 45° + x° ...(1)
In △OBP,
⇒ OB = BP ...(Given)
⇒ ∠OPB = ∠BOP (Angles opposite to equal sides are equal) ...(2)
From equation (1) and (2), we get:
⇒ ∠BOP = 45° + x° ...(3)
We know that,
Diagonals of square are perpendicular to each other.
∴ ∠BOC = 90°
⇒ ∠BOP + ∠POC = 90°
⇒ 45° + x° + x° = 90°
⇒ 2x° = 90° - 45°
⇒ 2x° = 45°
⇒ x° = `(45°)/2`
⇒ x° = `(22 1/2)^°`
⇒ ∠POC = `(22 1/2)^°`
Hence, proved that ∠POC = `(22 1/2)^°`
(ii) From figure,
⇒ ∠BDC = 45° ...(Diagonals of a square bisect the interior angles)
⇒ ∠BDC = 2 × `(22 1/2)^°`
⇒ ∠BDC = 2 × ∠POC
⇒ ∠BDC = 2 ∠POC
Hence, proved that ∠BDC = 2 ∠POC.
(iii) From equation (3),
⇒ ∠BOP = 45° + x°
⇒ ∠BOP = 45° + 22.5°
⇒ ∠BOP = 67.5°
⇒ ∠BOP = 3 × 22.5°
⇒ ∠BOP = 3 × ∠POC
⇒ ∠BOP = 3 ∠POC
Hence, proved that ∠BOP = 3 ∠COP.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
- ABCD is a square
- diagonal BD bisects ∠B as well as ∠D.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
In the following figures, ABCD is a parallelogram.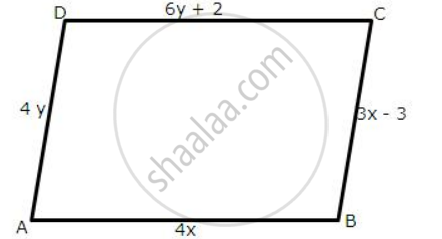
find the values of x and y.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
A rectangular floor 45 in long and 12 m broad is to be paved exactly with square tiles, of side 60 cm. Find the total number of tiles required to pave it.
If a carpet is laid on the floor such as a space of 50 cm exists between its edges and the edges of the floor, find what fraction of the floor is uncovered.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
A lawn in the shape of a rectangle is to be developed in front of a Marriage Hall. The length and breadth of the lawn are 44m and 32m. A space of 2m is left on the two shoulder sides and one longer side for flower and in the remaining area grass is laid. Calculate the area of the flower space and the area on which grass is laid.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
ABCD is a trapezium in which AB || DC and ∠A = ∠B = 45º. Find angles C and D of the trapezium.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Name polygon.

Make two more examples of this.
