Advertisements
Advertisements
प्रश्न
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
पर्याय
True
False
उत्तर
False
This is not true for any random quadrilateral. Observe the quadrilateral shown below.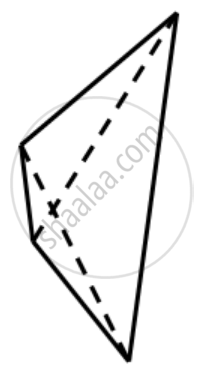
Clearly the diagonals of the given quadrilateral do not bisect each other. However, if the quadrilateral was a special quadrilateral like a parallelogram, this would hold true.
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.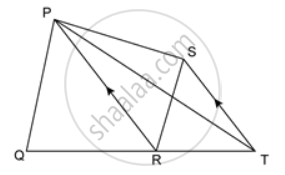
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN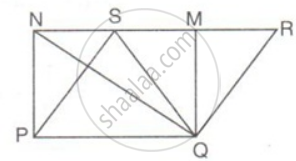
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Each angle of a rectangle is a right angle.
The opposite sides of a trapezium are parallel.
Give reason for the following :
A square can be thought of as a special rectangle.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?

Examine whether the following is a polygon. If it is not, say why?