Advertisements
Advertisements
प्रश्न
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
उत्तर
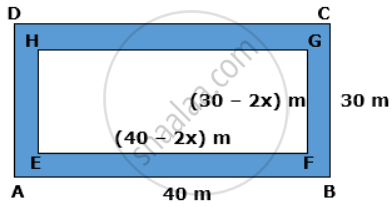
Let the given rectangular field be ABCD with length AB = 40m and width BC = 30m.
If the width of uniform path = x m,
the length of rectangle excluding path is EF = (40 - 2x) m and the width of rectangle excluding path is FG = (30 - 2x) m.
Now,
Area of rectangle ABCD -Area of rectangle EFGH = Area of path
⇒ (40 x 30) - [(40 - 2x) x (30 - 2x)] = 136
⇒ 1200 - [200 - 80x - 60x + 4x2] = 136
⇒ 1200 - 1200 + 140x - 4x2 = 136
⇒ 4x2 - 140x + 136 = 0
⇒ x2 - 35x + 34 = 0
⇒ x2 - 34x - x + 34 = 0
⇒ x(x - 34) -1(x - 34) = 0
⇒ (x - 34)(x - 1) = 0
⇒ x = 34 or x = 1
Rejected x = 34 (because it does not satisfy the calculation of the area of the path i.e. 136m2), we get x = 1
Thus, the width of the path is 1m.
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.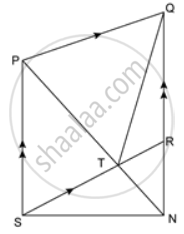
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.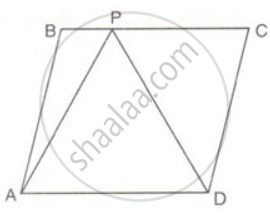
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.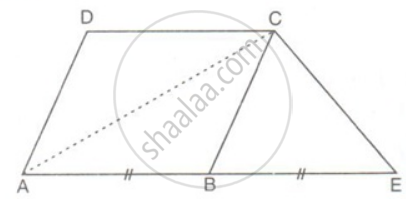
Find the area of each of the following figure:
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: area of the parallelogram.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
How many tiles, each of area 625 cm2, will be needed to pave a footpath which is 1 m wide and surrounds a grass plot of size 38 m x 14 m?
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Name polygon.
Make two more examples of this.
