Advertisements
Advertisements
प्रश्न
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.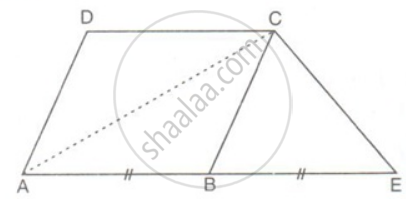
उत्तर
In parallelogram ABCD,
ar(ΔABC) = `(1)/(2)` x ar(parallelogram ABCD)
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
ar(parallelogram ABCD) = 2ar(ΔABC) ........(i)
In ΔACE,
ar(ΔACE) = ar(ΔABC) + ar(ΔBCE)
but ar(ΔABC) = ar(ΔBCE) ...(since BC is median)
ar(ΔACE) = 2ar(ΔABC) .........(ii)
From (i) and (ii)
ar(parallelogram ABCD) = ar(ΔACE).
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

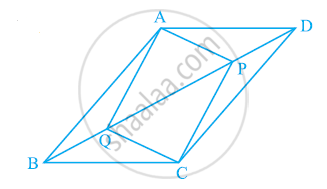
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.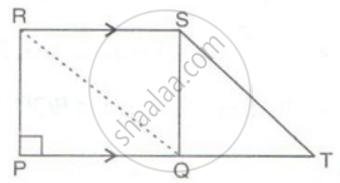
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.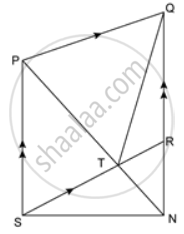
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.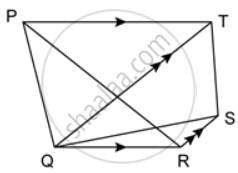
*Question modified
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure: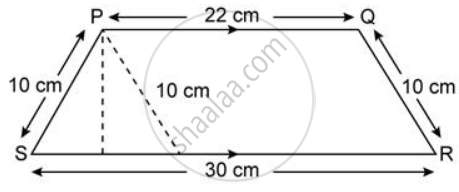
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Two adjacent sides of a parallelogram are 34 cm and 20 cm. If one of its diagonal is 42 cm, find: distance between its shorter sides
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
Each angle of a rectangle is a right angle.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Give reasons for the following :
A square can be thought of as a special rhombus.
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
