Advertisements
Advertisements
प्रश्न
Give reasons for the following :
A square can be thought of as a special rhombus.
उत्तर
- Because its all sides are equal and diagonals are perpendicular to each other.
- However, in case of a square, all interior angles are of 90º measure.
- A rhombus with each angle a right angle becomes a square. Therefore, a square can be thought of as a special rhombus.
APPEARS IN
संबंधित प्रश्न
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
In the following figures, ABCD is a parallelogram.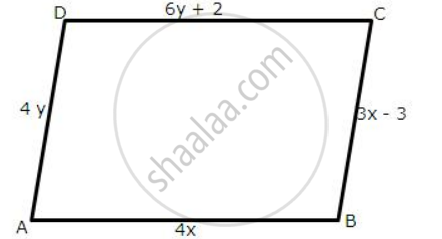
find the values of x and y.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.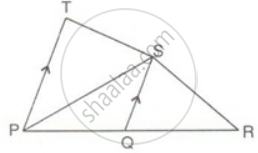
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
All the sides of a parallelogram are of equal length.
Give reason for the following :
A square can be thought of as a special rectangle.
Give reason for the following :
Square is also a parallelogram.
