Advertisements
Advertisements
प्रश्न
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
उत्तर
Opposite sides of a parallelogram are parallel and equal. In a rectangle, the opposite sides are parallel and equal. Also, all the interior angles of the rectangle are of the same measure, i.e., 90º. In other words, a parallelogram with each angle a right angle becomes a rectangle. Therefore, a rectangle can be thought of as a special parallelogram.
APPEARS IN
संबंधित प्रश्न
Show that the diagonals of a square are equal and bisect each other at right angles.
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.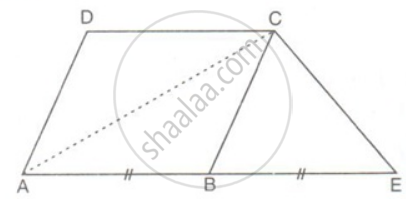
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
In a rectangle ABCD, AB = 7 cm and AD = 25 cm. Find the height of a triangle whose base is AB and whose area is two times the area of the rectangle ABCD.
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
A rectangular field is 240m long and 180m broad. In one corner a farm house is built on a square plot of side 40m. Find the area of the remaining portion and the cost of fencing the open sides Rs.25per m.
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
