Advertisements
Advertisements
प्रश्न
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD =
(b) Area of APQD = Area of BPQC
उत्तर
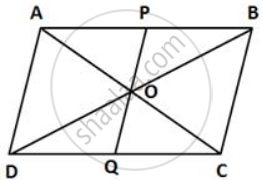
(a) A diagonal divides a parallelogram into two triangles of equal areas.
⇒ A(ΔADB) =
In ΔDOQ and ΔBOP,
∠DOQ = ∠BOP ...(Vertically opposite angles)
DO = BO ...(Diagonals of a || gm bisect each other)
∠ODQ = ∠OBP ...(Alternate angles)
∴ ΔDOQ ≅ ΔBOP ...(ASA test of congruency)
⇒ A(ΔDOQ) = A(ΔBOP)
Adding A(DOQ) on both sides, we get
A(ΔDOQ) + A(DOPA) = A(ΔBOP) + A(DOPA)
⇒ Area of APQD = A(ADB)
⇒ Area of APQD =
(b) A(ΔABC) =
In ΔCOQ and ΔAOP,
∠COQ = ∠AOP ...(Vertically opposite angles)
CCO = AO ...(Diagonals of a || gm bisect each other)
∠OCQ = ∠OAP ...(Alternate angles)
∴ ΔCOQ ≅ ΔAOP ...(ASA test of congruency)
⇒ A(ΔCOQ) = A(ΔAOP)
Adding A(COPB) on both sides, we get
A(ΔCOQ) + A(COPB) = A(ΔAOP) + A(COPB)
∴ Area of BPQC = A(ABC)
⇒ Area of BPQC =
∴ Area of APQD = Area of BPQC. ...[From (ii) and (iii)]
APPEARS IN
संबंधित प्रश्न
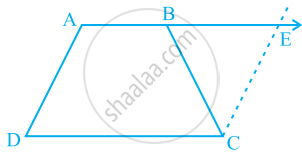
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.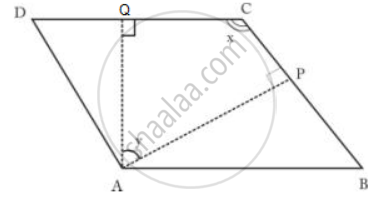
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the following figure, AE and BC are equal and parallel and the three sides AB, CD, and DE are equal to one another. If angle A is 102o. Find angles AEC and BCD.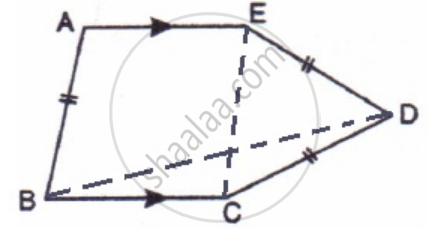
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.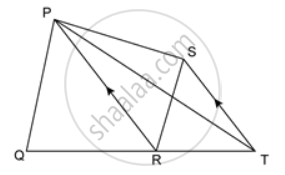
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN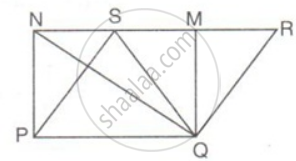
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
Find the area of each of the following figure: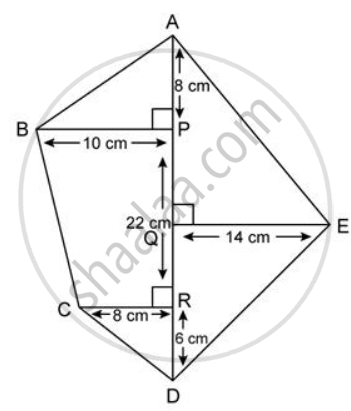
A rectangular floor 45 in long and 12 m broad is to be paved exactly with square tiles, of side 60 cm. Find the total number of tiles required to pave it.
If a carpet is laid on the floor such as a space of 50 cm exists between its edges and the edges of the floor, find what fraction of the floor is uncovered.
Find the perimeter and area of a square whose diagonal is
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
PQRS is a square with each side 6cm. T is a point on QR such that the
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
Give reasons for the following :
A square can be thought of as a special rhombus.
