Advertisements
Advertisements
प्रश्न
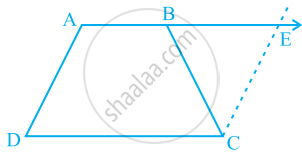
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
उत्तर
We have given a trapezium ABCD in which AB || CD and AD = BC.
(i) Produce AB to E and draw CE || AD ...(1)
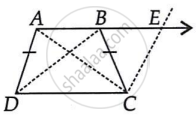
∵ AB || DC ⇒ AE || DC
Also, AD || CE ...[From (1)]
∴ AECD is a parallelogram.
⇒ AD = CE ...(1) ...[∵ Opposite sides of the parallelogram are equal]
But AD = BC ...(2) ...[Given]
By (1) and (2), BC = CE
Now, in ΔBCE, we have BC = CE
⇒ ∠CEB = ∠CBE ...(3) ...[∵ Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180° ...(4) ...[Linear pair]
and ∠A + ∠CEB = 180° ...(5) ...[Co-interior angles of a parallelogram ADCE]
From (4) and (5), we get
∠ABC + ∠CBE = ∠A + ∠CEB
∠ABC = ∠A ...[From (3)]
∠B = ∠A ...(6)
(ii) AB || CD and AD is a transversal.
∴ ∠A + ∠D = 180° ...(7) ...[Co-interior angles]
Similarly, ∠B + ∠C = 180° ...(8)
From (7) and (8), we get
∠A + ∠D = ∠B + ∠C
∠C = ∠D ...[From (6)]
(iii) In ΔABC and ΔBAD, we have
AB = BA ...[Common]
BC = AD ...[Given]
∠ABC = ∠BAD ...[Proved]
∴ ΔABC ≅ ΔBAD ...[By SAS congruency]
(iv) Since, ΔABC ≅ ΔBAD ...[Proved]
AC = BD ...[By C.P.C.T.]
APPEARS IN
संबंधित प्रश्न
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.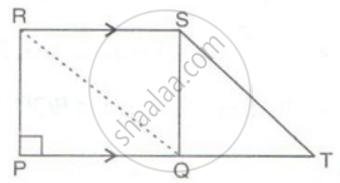
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
The length of a rectangular field is thrice of its width. If the perimeter of this field is 1.6km, find its area in sq.m.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
In quadrilateral ABCD, ∠A + ∠D = 180º. What special name can be given to this quadrilateral?
Examine whether the following is a polygon. If it is not, say why?

