Advertisements
Advertisements
प्रश्न
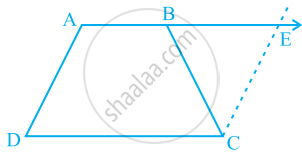
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
उत्तर
We have given a trapezium ABCD in which AB || CD and AD = BC.
(i) Produce AB to E and draw CE || AD ...(1)
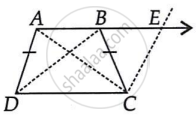
∵ AB || DC ⇒ AE || DC
Also, AD || CE ...[From (1)]
∴ AECD is a parallelogram.
⇒ AD = CE ...(1) ...[∵ Opposite sides of the parallelogram are equal]
But AD = BC ...(2) ...[Given]
By (1) and (2), BC = CE
Now, in ΔBCE, we have BC = CE
⇒ ∠CEB = ∠CBE ...(3) ...[∵ Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180° ...(4) ...[Linear pair]
and ∠A + ∠CEB = 180° ...(5) ...[Co-interior angles of a parallelogram ADCE]
From (4) and (5), we get
∠ABC + ∠CBE = ∠A + ∠CEB
∠ABC = ∠A ...[From (3)]
∠B = ∠A ...(6)
(ii) AB || CD and AD is a transversal.
∴ ∠A + ∠D = 180° ...(7) ...[Co-interior angles]
Similarly, ∠B + ∠C = 180° ...(8)
From (7) and (8), we get
∠A + ∠D = ∠B + ∠C
∠C = ∠D ...[From (6)]
(iii) In ΔABC and ΔBAD, we have
AB = BA ...[Common]
BC = AD ...[Given]
∠ABC = ∠BAD ...[Proved]
∴ ΔABC ≅ ΔBAD ...[By SAS congruency]
(iv) Since, ΔABC ≅ ΔBAD ...[Proved]
AC = BD ...[By C.P.C.T.]
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle with ∠ABD = 40°. Determine ∠DBC .
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
A footpath of uniform width runs all around the inside of a rectangular garden of 40 m x 30 m. If the path occupies 136 m2, find the width of the path.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Give reason for the following :
Square is also a parallelogram.
Examine whether the following is a polygon. If it is not, say why?

