Advertisements
Advertisements
Question
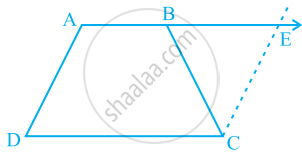
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
- ∠A = ∠B
- ∠C = ∠D
- ΔABC ≅ ΔBAD
- diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
Solution
We have given a trapezium ABCD in which AB || CD and AD = BC.
(i) Produce AB to E and draw CE || AD ...(1)
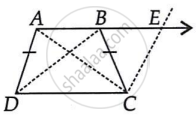
∵ AB || DC ⇒ AE || DC
Also, AD || CE ...[From (1)]
∴ AECD is a parallelogram.
⇒ AD = CE ...(1) ...[∵ Opposite sides of the parallelogram are equal]
But AD = BC ...(2) ...[Given]
By (1) and (2), BC = CE
Now, in ΔBCE, we have BC = CE
⇒ ∠CEB = ∠CBE ...(3) ...[∵ Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180° ...(4) ...[Linear pair]
and ∠A + ∠CEB = 180° ...(5) ...[Co-interior angles of a parallelogram ADCE]
From (4) and (5), we get
∠ABC + ∠CBE = ∠A + ∠CEB
∠ABC = ∠A ...[From (3)]
∠B = ∠A ...(6)
(ii) AB || CD and AD is a transversal.
∴ ∠A + ∠D = 180° ...(7) ...[Co-interior angles]
Similarly, ∠B + ∠C = 180° ...(8)
From (7) and (8), we get
∠A + ∠D = ∠B + ∠C
∠C = ∠D ...[From (6)]
(iii) In ΔABC and ΔBAD, we have
AB = BA ...[Common]
BC = AD ...[Given]
∠ABC = ∠BAD ...[Proved]
∴ ΔABC ≅ ΔBAD ...[By SAS congruency]
(iv) Since, ΔABC ≅ ΔBAD ...[Proved]
AC = BD ...[By C.P.C.T.]
APPEARS IN
RELATED QUESTIONS
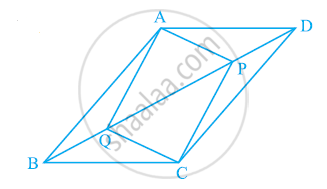
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
In a square ABCD, diagonals meet at O. P is a point on BC such that OB = BP.
Show that:
- ∠POC = `[ 22 ( 1°)/( 2 ) ]`
- ∠BDC = 2 ∠POC
- ∠BOP = 3 ∠CPO
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.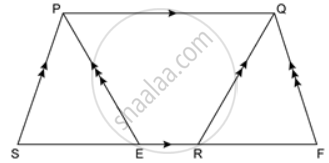
Find the area of each of the following figure:
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
Find the area of a rhombus whose perimeter is 260cm and the length of one of its diagonal is 66cm.
Examine whether the following is a polygon. If it is not, say why?

