Advertisements
Advertisements
Question
The angles of a quadrilateral are in the ratio 3: 4: 5: 6. Show that the quadrilateral is a trapezium.
Solution
Given that the angles of a quadrilateral are in the ratio 3:4:5:6
Let the angles be 3x, 4x, 5x, 6x.
3x + 4x + 5x + 6x = 360°
⇒ x = `(360°)/18`
⇒ x = 20°
Therefore the angles are
3 x 20 = 60°
4 x 20 = 80°
5 x 20 = 100°
6 x 20 = 120°
Since all the angles are of different degrees thus forms a trapezium.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
In the figure, given below, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that: ∠AMD = 90°.

In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.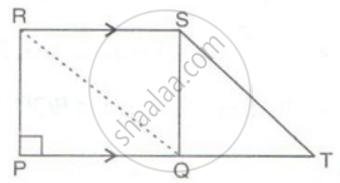
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.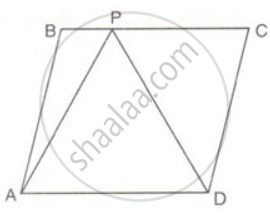
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.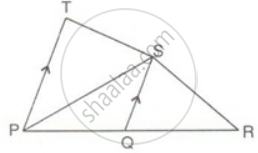
Find the area of each of the following figure:
Find the height of a parallelogram whose area is 144cm2 and the base is 18cm.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
The diagonals of a square are perpendicular to one another.
