Advertisements
Advertisements
Question
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.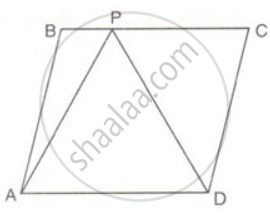
Solution
ar(ΔAPD) = `(sqrt(3)"s"^2)/(4)`
ar(ΔAPD) = `(sqrt(3) xx 8^2)/(4)`
ar(ΔAPD) = `(sqrt(3) xx 64)/(4)`
ar(ΔAPD) = `sqrt(3) xx 16 = 16sqrt(3)"cm"^2`
ar(ΔAPD) = `(1)/(2)` x ar(parallelogram ABCD)
(The area of a triangle is half that of a parallelogram on the same base and between the same parallels)
⇒ ar(parallelogram ABCD) = 2 x ar(ΔAPD)
⇒ ar(parallelogram ABCD) = 2 x `16sqrt(3)"cm"^2`
⇒ ar(parallelogram ABCD) = `32sqrt(3)"cm"^2`.
APPEARS IN
RELATED QUESTIONS
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
If two adjacent sides of a parallelogram are equal, it is a rhombus.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.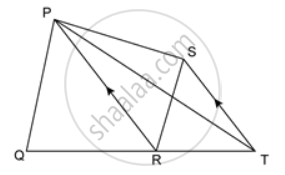
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
Find the area of each of the following figure:
Find the area of each of the following figure: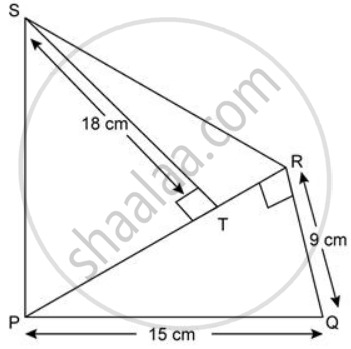
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
In a trapezium the parallel sides are 12cm and 8cm. If the distance between them is 6cm, find the area of the trapezium.
Find the perimeter of a rhombus whose diagonals are 24cm and 10cm.
The perimeter of a square plot of land is 64m. The area of a nearby rectangular plot is 24m2 more than the area of the given square. If the length of the rectangle is 14m, find its breadth.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
Give reason for the following :
Square is also a parallelogram.
Examine whether the following is a polygon. If it is not, say why?

Examine whether the following is a polygon. If it is not, say why?