Advertisements
Advertisements
Question
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
Solution
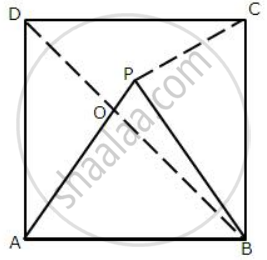
In the given figure ΔAPB is an equilateral triangle.
Therefore all its angles are 60°
Again in the
ΔADB,
∠ABD = 45°
∠AOB = 180° - 60° - 45° = 75°
Again
ΔBPC
⇒ ∠BPC = 75° ....[ Since BP = CB ]
Now,
∠C = ∠BCP + ∠PCD
⇒ ∠PCD = 90° - 75°
⇒ ∠PCD = 15°
Therefore,
∠APC = 60° + 75°
⇒ ∠APC = 135°
⇒ Reflex ∠APC = 360° - 135° = 225°
(i) ∠AOB = 75°
(ii) ∠BPC = 75°
(iii) ∠PCD = 15°
(iv) Reflex ∠APC = 225°
APPEARS IN
RELATED QUESTIONS
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

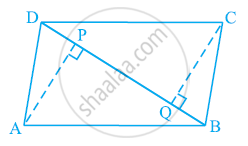
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
- ΔAPB ≅ ΔCQD
- AP = CQ
State, 'true' or 'false'
The diagonals of a parallelogram bisect each other at right angle.
State, 'true' or 'false'
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.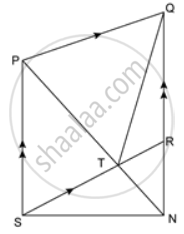
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
Find the area of each of the following figure: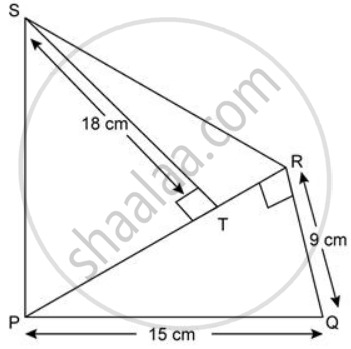
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
The area of a floor of a rectangular room is 360m2. If its length is 24cm, find its perimeter.
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
A rectangular hall of 40m by 24m is covered with carpets of size 6m x 4m. Find the number of carpets required to cover the hall.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Find the perimeter and area of a square whose diagonal is `5sqrt(2)"cm"`. Give your answer correct to two decimal places if `sqrt(2)` = 1.414.
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
A rectangular field is 80m long and 50m wide. A 4m wide runs through the centre of the field parallel to the length and breadth of the field. Find the total area of the roads.
Examine whether the following is a polygon. If it is not, say why?

