Advertisements
Advertisements
प्रश्न
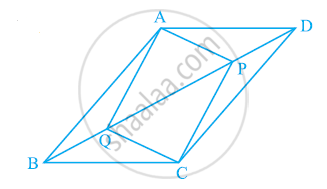
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see the given figure). Show that:
- ΔAPD ≅ ΔCQB
- AP = CQ
- ΔAQB ≅ ΔCPD
- AQ = CP
- APCQ is a parallelogram
उत्तर
(i) In ΔAPD and ΔCQB,
∠ADP = ∠CBQ ...(Alternate interior angles for BC || AD)
AD = CB ...(Opposite sides of parallelogram ABCD)
DP = BQ ...(Given)
∴ ΔAPD ≅ ΔCQB ...(Using SAS congruence rule)
(ii) As we had observed that ΔAPD ≅ ΔCQB,
∴ AP = CQ ...(CPCT)
(iii) In ΔAQB and ΔCPD,
∠ABQ = ∠CDP ...(Alternate interior angles for AB || CD)
AB = CD ...(Opposite sides of parallelogram ABCD)
BQ = DP ...(Given)
∴ ΔAQB ≅ ΔCPD ...(Using SAS congruence rule)
(iv) As we had observed that ΔAQB ≅ ΔCPD,
∴ AQ = CP ...(CPCT)
(v) From the results obtained in (ii) and (iv),
AQ = CP and
AP = CQ
Since opposite sides in quadrilateral APCQ are equal to each other, APCQ is a parallelogram.
APPEARS IN
संबंधित प्रश्न
In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.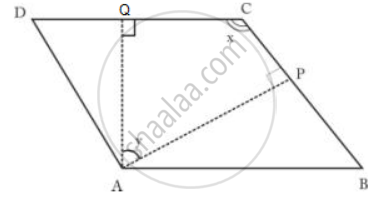
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
The given figure shows a square ABCD and an equilateral triangle ABP. 
Calculate: (i) ∠AOB
(ii) ∠BPC
(iii) ∠PCD
(iv) Reflex ∠APC
Find the area of quadrilateral, whose diagonals of lengths 18 cm and 13 cm intersect each other at right angle.
Find the perimeter and area of a rectangle whose length and breadth are 12cm and 9cm respectively.
A rectangular field 240m long has an area 36000m2. Find the cost of fencing the field at Rs.2.50per m.
Inside a square field of side 44m, a square flower bed is prepared leaving a graved path all round the flower bed. The total cost of laying the flower bed at Rs.25per sq m. and gravelling the path at Rs.120per sq m. is Rs.80320. Find the width of the gravel path.
All the sides of a parallelogram are of equal length.
Give reasons for the following :
A square can be thought of as a special rhombus.
